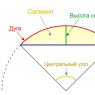
Нахождение дуги окружности. Окружность

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

Окружность — линия, ограничивающая круг.
Дуга — часть окружности.
Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
Хорда — отрезок, соединяющий две точки окружности.
Сегмент — часть круга, ограниченная хордой и дугой.
Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

; длина хорды ;
высота сегмента ; центральный угол .

2. Даны диаметр D и длина хорды X

; длина дуги ;
высота сегмента ; центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

3. Даны диаметр D и центральный угол φ

; длина дуги ;
длина хорды ; высота сегмента .

4. Даны диаметр D и высота сегмента H

; длина дуги ;
длина хорды ; центральный угол .

6. Даны длина дуги L и центральный угол φ

; диаметр ;
длина хорды ; высота сегмента .

8. Даны длина хорды X и центральный угол φ

; длина дуги ;
диаметр ; высота сегмента .

9. Даны длина хорды X и высота сегмента H

; длина дуги ;
диаметр ; центральный угол .

10. Даны центральный угол φ и высота сегмента H

; диаметр ;
длина дуги ; длина хорды .

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем . Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Окружность - основная фигура в геометрии, свойства которой рассматривают в школе в 8 классе. Одна из типичных задач, связанных с окружностью, заключается в нахождении площади некоторой ее части, которая носит название кругового сектора. В статье приводятся формулы площади сектора и длины его дуги, а также пример их использования для решения конкретной задачи.

Понятие об окружности и круге

Перед тем как приводить формулу площади сектора окружности, рассмотрим, что собой представляет указанная фигура. Согласно математическому определению, под окружностью понимают такую фигуру на плоскости, все точки которой равноудалены от некоторой одной точки (центра).

Когда рассматривают окружность, то пользуются следующей терминологией:

Радиус - отрезок, который проводится от центральной точки до кривой окружности. Его принято обозначать буквой R.
Диаметр - это отрезок, который соединяет две точки окружности, но при этом проходит также через центр фигуры. Его обычно обозначают буквой D.
Дуга - это часть кривой окружности. Измеряют ее либо в единицах длины, либо с использованием углов.

Круг - еще одна важная фигура геометрии, он представляет собой совокупность точек, которая ограничена кривой окружности.

Площадь круга и длина окружности

Отмеченные в названии пункта величины рассчитываются с использованием двух простых формул. Они приведены ниже:

Длина окружности: L = 2*pi*R.
Площадь круга: S = pi*R 2 .

В этих формулах pi - это некоторая константа, которая называется числом Пи. Оно является иррациональным, то есть не может быть точно выражено простой дробью. Приблизительно число Пи равно 3,1416.

Как видно из приведенных выражений, чтобы рассчитать площадь и длину достаточно знать только радиус окружности.

Площадь сектора круга и длина его дуги

Перед тем как рассматривать соответствующие формулы, напомним, что угол в геометрии принято выражать двумя основными способами:

в шестидесятеричных градусах, причем полный оборот вокруг своей оси равен 360 o ;
в радианах, которые выражаются в долях числа pi и связаны с градусами следующим равенством: 2*pi = 360 o .

Сектор круга - это фигура, ограниченная тремя линиями: дугой окружности и двумя радиусами, находящимися на концах этой дуги. Пример кругового сектора изображен на фото ниже.

Получив представление о том, что такое сектор для круга, легко понять, как вычислить его площадь и длину соответствующей дуги. Из рисунка выше видно, что дуге сектора соответствует угол θ. Мы знаем, что полная окружность соответствует 2*pi радианам, значит, формула площади кругового сектора примет вид: S 1 = S*θ/(2*pi) = pi*R 2 *θ/(2*pi) = θ*R 2 /2. Здесь угол θ выражен в радианах. Аналогичная формула площади сектора в случае, если угол θ измеряется в градусах, будет иметь вид: S 1 = pi*θ*R 2 /360.

Длина дуги, образующей сектор, вычисляется по формуле: L 1 = θ*2*pi*R/(2*pi) = θ*R. И если θ известен в градусах, тогда: L 1 = pi*θ*R/180.

Пример решения задачи

Покажем на примере простой задачи, как пользоваться формулами площади сектора круга и длины его дуги.

Известно, что колесо имеет 12 спиц. Когда колесо делает один полный оборот, то оно преодолевает расстояние 1,5 метра. Чему равна площадь, заключенная между двумя соседними спицами колеса, и чему равна длина дуги между ними?

Как видно из соответствующих формул, чтобы ими пользоваться, необходимо знать две величины: радиус окружности и угол дуги. Радиус можно вычислить, исходя из знания длины окружности колеса, поскольку пройденное им расстояние за один оборот, точно ей соответствует. Имеем: 2*R*pi = 1,5, откуда: R = 1,5/(2*pi) = 0,2387 метра. Угол между ближайшими спицами можно определить, зная их число. Полагая, что все 12 спиц делят равномерно круг на равные сектора, мы получаем 12 одинаковых секторов. Соответственно, угловая мера дуги между двумя спицами равна: θ = 2*pi/12 = pi/6 = 0,5236 радиан.

Мы нашли все необходимые величины, теперь их можно подставить в формулы и посчитать требуемые условием задачи значения. Получаем: S 1 = 0,5236*(0,2387) 2 /2 = 0,0149 м 2, или 149 см 2 ; L 1 = 0,5236*0,2387 = 0,125 м, или 12,5 см.

Изначально это выглядит так:

Рисунок 463.1 . а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.

Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.

Решение подобной задачи достаточно подробно рассматривалось в статье "Расчет арочной перемычки ", поэтому здесь лишь приведу основные формулы:

tg(a /4) = 2Н/L (278.1.2)

а /4 = arctg(2H/L )

R = H /(1 - cos(a /2)) (278.1.3)

Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.

А теперь поговорим о недостатках.

Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад - для того, чтобы напомнить формулы - есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.

Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.

Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.

В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.

Второй метод определения радиуса дуги (метод последовательных приближений)

Итак продолжим рассмотрение имеющейся ситуации.

Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.

Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.

Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше - то искомый центр дуги выше на прямой.

Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.

Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.

Теоретически это выглядит примерно так:

Рисунок 463.2 . Определение центра дуги методом последовательных приближений.

А на практике примерно так:

Фотография 463.1 . Разметка заготовки сложной формы с разными радиусами.

Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Формула для нахождения длины дуги окружности довольно проста, и очень часто на важных экзаменах типа ЕГЭ встречаются такие задачи, которые невозможно решить без ее применения. Также необходимо ее знать для сдачи международных стандартизированных тестов, например SAT и других.

Чему равна длина дуги окружности?

Формула выглядит следующим образом:

l = πrα / 180°

Что собой представляет каждый из элементов формулы:

π - число Пи (постоянная величина, равная ≈ 3,14);
r - радиус данной окружности;
α - величина угла, на который опирается дуга (центральный, а не вписанный).

Как видно, чтобы решить задачу, в условии должны присутствовать r и α. Без этих двух величин длину дуги найти невозможно.

Каким образом выводится эта формула и почему она так выглядит?

Все предельно легко. Станет намного понятнее, если в знаменателе поставить 360°, а в числителе спереди добавить двойку. Также можно α не оставить в дроби, вывести ее и написать со знаком умножения. Это вполне можно себе позволить, так как данный элемент стоит в числителе. Тогда общий вид станет таким:

l = (2πr / 360°) × α

Просто для удобства сократили 2 и 360°. А теперь, если приглядеться, то можно заметить очень знакомую формулу длины всей окружности, а именно - 2πr. Весь круг состоит из 360°, потому мы делим полученную меру на 360 частей. Затем мы умножаем на число α, то есть на то количество "кусков пирога", которое нам требуется. Но всем доподлинно известно, что число (то есть длина всей окружности) не может делиться на градус. Что же делать в таком случае? Обычно, как правило, градус сокращается с градусом центрального угла, то есть с α. После же остаются только числа, а в итоге получается конечный ответ.

Этим можно объяснить то, почему длина дуги окружности находится таким образом и имеет такой вид.

Пример задачи средней сложности с применением данной формулы

Условие: Имеется окружность с радиусом 10 сантиметров. Градусная мера центрального угла составляет 90°. Найти длину дуги окружности, образованную этим углом.

Решение: l = 10π × 90° / 180° = 10π × 1 / 2=5π

Ответ: l = 5π

Также возможно, чтоб вместо градусной меры давалась бы радианная мера угла. Ни в коем случае не стоит пугаться, ведь на сей раз задача стала намного легче. Чтобы перевести радианную меру в градусную, нужно данное число умножить на 180° / π. Значит, теперь можно подставить вместо α следующую комбинацию: m × 180° / π. Где m - это радианное значение. А дальше 180 и число π сокращаются и получается совершенно упрощенная формула, которая выглядит следующим образом:

m - радианная мера угла;
r - радиус данной окружности.